DAY 5 試題

問題描述

給定一個已連通的無向圖中的某個節點的引用，我們需要返回該圖的深度拷貝（克隆）。這裡的每個節點包含一個整數值 val 以及一個鄰居列表 neighbors，其中鄰居列表中包含了與該節點相連的其他節點。

節點類別的定義如下：

class Node {
public:
    int val;
    vector<Node*> neighbors;
};

測試資料使用鄰接列表表示圖結構，且輸入中的第一個節點的值總是等於 1，我們需要返回此圖的深度拷貝。
範例：

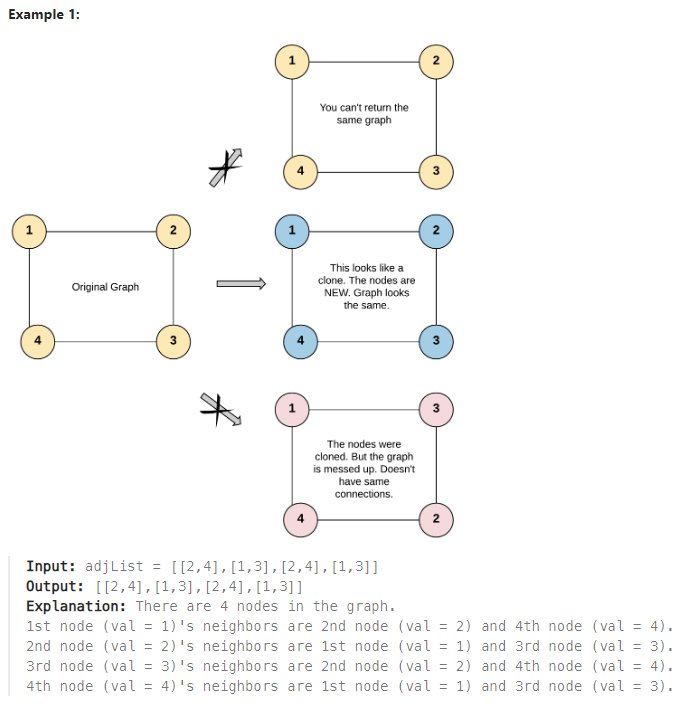
輸入: adjList = [[2,4],[1,3],[2,4],[1,3]]
輸出: [[2,4],[1,3],[2,4],[1,3]]

輸入: adjList = [[]]
輸出: [[]]

輸入: adjList = []
輸出: []

解題思路

這題要求我們對一個圖進行深度拷貝，因此需要理解圖的遍歷方式。我們可以使用深度優先搜索（DFS）或廣度優先搜索（BFS）來實現。

具體步驟如下：

1. 圖的遍歷與節點複製：

• 使用 DFS 或 BFS 從給定的節點開始遍歷整個圖，並逐步複製每一個節點。
• 為了避免重複拷貝節點，使用一個哈希表來存儲每個節點與其克隆節點的對應關係。

2. 處理節點的鄰居：

• 在每個節點被克隆後，我們需要對其鄰居節點進行遞歸處理。如果鄰居節點尚未克隆，我們會進行克隆並記錄在哈希表中；如果已經克隆過，我們直接使用該克隆節點。

3. 處理特例：

• 如果圖是空的，直接返回空。
• 如果節點只有自己但沒有鄰居，也需要處理。

class Solution {
private:
    unordered_map<Node*, Node*> cloned;

    // DFS 遞歸函數
    Node* dfs(Node* node) {
        if (!node) return nullptr;

        // 如果節點已經被克隆，則直接返回
        if (cloned.find(node) != cloned.end()) {
            return cloned[node];
        }

        // 克隆當前節點
        Node* copy = new Node(node->val);
        cloned[node] = copy;

        // 遍歷鄰居並克隆
        for (Node* neighbor : node->neighbors) {
            copy->neighbors.push_back(dfs(neighbor));
        }

        return copy;
    }

public:
    Node* cloneGraph(Node* node) {
        return dfs(node);
    }
};

解法重點與分析

哈希表的應用：

• 哈希表用來儲存每個節點與其對應的克隆節點，這樣可以有效避免重複克隆，減少不必要的計算。

DFS 遍歷：

• 使用 DFS 進行遞歸遍歷，從起始節點出發，依次克隆每個節點及其鄰居，直至遍歷完整個圖。

特例處理：

• 當輸入圖為空時，直接返回 nullptr，這是必要的邊界條件處理。

總結與為何使用DFS而非BFS?

透過深度優先搜索（DFS）來實現圖的深度拷貝是一個簡潔且有效的解法。DFS 的遞歸特性非常適合逐步克隆每個節點及其鄰居，並且利用哈希表來避免重複克隆。相比廣度優先搜索（BFS），DFS 在實現上更加簡單直觀，特別是當我們使用遞歸處理時，可以自然地處理每個節點的鄰居，而不需要額外的隊列來控制節點的順序。因此，在這種情況下，DFS 是一個更為合適的選擇，能夠更清晰地表達圖的遍歷與克隆過程。

以上是第五天的自學內容分享，謝謝大家。